36- Redondeo Numérico (Parte I)
Fuente:
https://answers.microsoft.com/es-es/msoffice/forum/all/redondeo/df0d58ff-11d6-40db-9137-a4ea0ea3fe73
Resumen
Nivel técnico: Intermedio Se
aplica a: cualquier versión de
Office. Pretende explicar algo
aparentemente sencillo pero que
tiene su complicación: el
redondeo de cantidades
numéricas.
¿Qué es el redondeo?
Según la Real Academia Española,
redondear una cantidad es
prescindir de pequeñas
diferencias en más o en menos,
para tener en cuenta solamente
unidades de orden superior.
Por ejemplo, en el sistema
decimal, redondeamos a unidades,
a decenas, a centenas, o a
décimas, centésimas, milésimas,…
Con el redondeo o se pierde
precisión (por ejemplo, una
medida con precisión de
centímetros, 1,03 m., redondeada
a 1 m.) o se pretende expresar
la precisión del dato (si
medimos una distancia y la
precisión de las medidas o de
los cálculos establecen una
precisión de centenas tenemos
que redondear a las centenas, o,
si en un cálculo con la unidad
monetaria euro, una operación
matemática produce un resultado
con más de dos decimales,
obligatoriamente tendremos que
redondear a dos decimales, pues
la moneda más pequeña es el
céntimo). Esto es importante:
cuando redondeamos 1,03 no
debemos redondear a 1,00, sino a
1,0 o a 1, pues las cifras
decimales indican la precisión
de la medida (no es lo mismo
decir que algo mide 1,00 m., que
1,0 m., que 1 m.; la primera de
las medidas tiene precisión de
centímetros, las otras no).
¿Por qué redondeamos?
El redondeo se hace por
conveniencia o por necesidad.
Se redondea por conveniencia
cuando no necesitamos mucha
precisión en los cálculos
(trabajar con números
redondeados es menos costoso en
tiempo y facilidad de cálculo) o
en el valor del dato (un número
redondeado es más claro y fácil
de recordar) o para indicar la
precisión de un dato (no tiene
sentido hacer una estimación del
número de asistentes a un acto
multitudinario y decir que había
123.456 personas, en función de
la precisión de la estimación
diríamos 100.000 o 120.000).
Se redondea por necesidad cuando
trabajamos con un número
irracional o periódico (estos
números tienen infinitas cifras)
o cuando tenemos limitado el
número de cifras con las que
podemos trabajar (es el caso de
las operaciones que se hacen en
una calculadora u ordenador, o
el caso de la notación interna
de los números en punto
flotante) o cuando el número de
cifras nos lo impone la unidad
de medida (cuando trabajamos con
cifras de dinero en euros, no
podemos dar una cifra inferior
al céntimo, pues es la moneda
más pequeña que existe).
Métodos de redondeo:
No existe una única manera de
redondear un número y a un
entero que, en consecuencia, el
redondeo dependerá de cómo
definamos la operación de
redondeo.
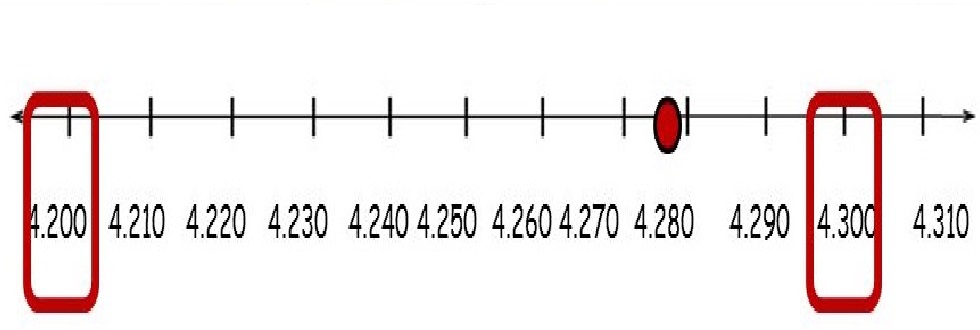
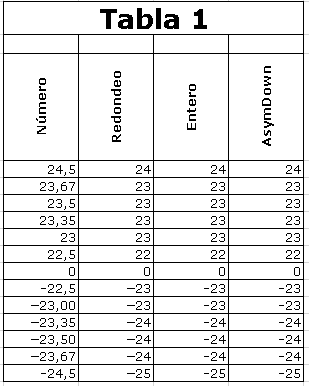
Redondeo acercándose a -¥
(Round Down)
que es el primer entero que nos
encontramos, recorriendo la
recta de los números reales en
sentido hacia -¥, partiendo de
y. Dicho de otro modo, que es el
mayor entero
que no excede y.
La función ENTERO de Excel
utiliza este método de redondeo,
así como la función
personalizada AsymDown.
La función Floor de Excel
no funciona de acuerdo con la
definición matemática de la
función suelo (Floor).
Números que son iguales en valor
absoluto, no son redondeados de
igual modo, a esto se le dice
comportamiento asimétrico.
Redondeo acercándose a +¥
(Round Up)
que es primer entero que nos
encontramos, recorriendo la
recta de los números reales, en
sentido hacia +¥, partiendo de
y. Dicho de otro modo, que es el
menor entero que no es menor que
y.
No existe ninguna función Excel
que haga este redondeo. La
función Ceiling de Excel
no funciona de acuerdo con la
definición matemática de la
función techo (ceil).
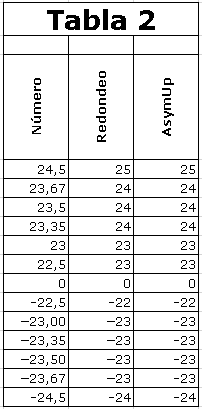
Números que son iguales en valor
absoluto, no son redondeados de
igual modo, a esto se le dice
comportamiento asimétrico.
Redondeo acercándose a cero (Round
Towards Zero)
que es el primer entero que nos
encontramos, partiendo de y,
recorriendo la recta de los
números reales, en sentido hacia
0. Dicho de otro modo, que es la
parte entera de y, sin sus
dígitos fraccionarios.
Este método es el que utilizamos
cuando truncamos un número (nos
quedamos sólo con la parte
entera).
La función TRUNCAR de Excel, la
función Floor de VBA
Excel y las funciones
personalizadas RoundDown
y SymDown, utiliza este
método de redondeo.
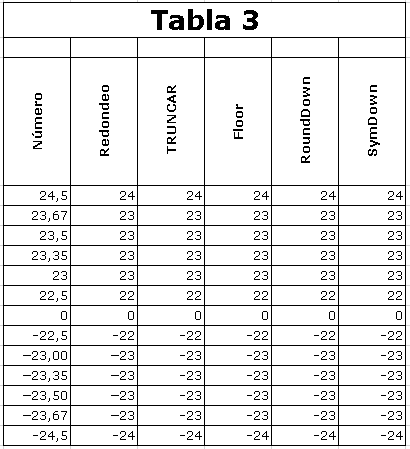
Números que son iguales en valor
absoluto, también son iguales en
valor absoluto una vez
redondeados. Comportamiento
simétrico.
Redondeo alejándose de cero (Round
Away From Zero)
que es el primer entero que nos
encontramos, partiendo de y,
recorriendo la recta de los
números reales, alejándonos del
0. Dicho de otro modo, si y es
un entero, que es y, en caso
contrario que es el entero más
cercano a 0 y tal que y esté
entre 0 y que.
La función REDONDEAR.MAS
de Excel, la función Ceiling
de VBA Excel y las funciones
personalizadas RoundUp y
SymUp, utilizan este
redondeo.
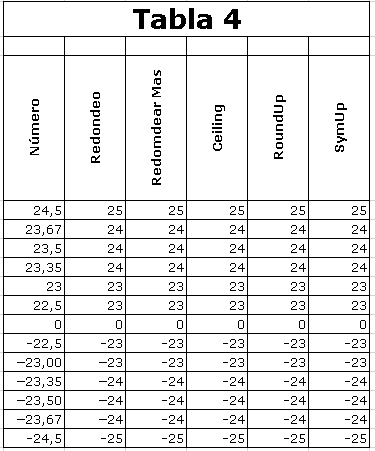
Números que son iguales en valor
absoluto, también son iguales en
valor absoluto una vez
redondeados. Comportamiento
simétrico.
Redondeo al más cercano (Round
To Nearest) que es el entero
más cercano a y.
En este método se plantea el
dilema de cómo redondear un
número que está, exactamente, a
medio camino de dos números
enteros (es el caso del número
23,50, está a la misma distancia
de 23 que de 24). Para resolver
este dilema se utilizan
distintas reglas de desempate.
Desempate la mitad hacia arriba
(Round Half Up)
La regla de desempate, redondear
la mitad hacia arriba (Round
Half Up), o redondear la
mitad hacia más infinito (Round
Half Towards Plus Infinity),
se usa ampliamente en muchas
disciplinas y consiste en que,
cuando y está a mitad de camino,
se redondea hacia arriba.
No existe ninguna función Excel
que haga este redondeo, sólo la
función personalizada
AsymArith lo hace.
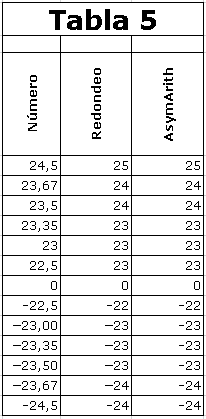
Los números que son iguales en
valor absoluto también son
iguales en valor absoluto una
vez redondeados, excepto los que
están a medio camino.
Ahora supongamos que tenemos que
sumar una relación
suficientemente larga de números
aleatorios, si hay números
positivos y negativos, la suma
de estos números redondeados,
tenderá a ser igual a la suma de
los números originales (sin
redondear), porque los redondeos
se compensarán, pero, si la
relación la forman números
mayoritariamente positivos, como
la fracción 0,5 siempre se
redondea hacia arriba, la suma
tenderá a ser mayor que la de
los números originales (por
exceso o con sesgo positivo). En
sentido contrario si la relación
es de números mayoritariamente
negativos.
Este error de redondeo, en
determinados casos iterativos y
si no se utiliza adecuadamente
la función de redondeo, puede
llegar a ser inaceptable. Por
ejemplo: cuando se creó la Bolsa
de Vancouver (Vancouver Stock
Exchange) en 1982, iniciaron el
índice a 1.000,000 (tres cifras
decimales), y después de 22
meses, el índice había caído a
cerca de 520 mientras los
precios de las acciones se
habían incrementado en el mismo
periodo. El problema se debió a
que el índice se recalculaba
miles de veces al día, y siempre
se redondeaba a 3 decimales, de
tal manera que los errores de
redondeo se acumulaban.
Recalculando con mejores métodos
el valor del índice, para el
mismo periodo, fue 1.098,892.
Otro ejemplo:
2,00 + 0,555 = 2,56
2,56 – 0,555 = 2,01
2,01 + 0,555 = 2,57
2,57 – 0,555 = 2,02
Vemos que el resultado, después
de sumar y restar la misma
cantidad, no es el de partida y
si repetimos el proceso el error
se incrementará sin límite. En
este caso, lo correcto es no
redondear después de cada suma,
sino al final del proceso.
Desempate la mitad hacia abajo (Round
Half Down)
No existe ninguna función de
Excel que realice este redondeo.
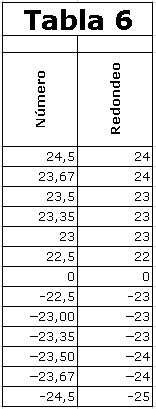
Por ejemplo, 23,5 se redondea a
23, y −23.5 se redondea a −24.
Es de aplicación lo dicho en el
caso anterior mutatis mutandi.
Desempate la mitad alejándose
del cero (Round Half Away
From Zero o Round Half
Towards Infinity)
Cuando damos formato de decimales a un número en Excel, las funciones de Excel REDONDEAR y REDOND.MULT, la función Round de VBA Excel, y las funciones personalizadas MRound y SymArith, realizan este redondeo.
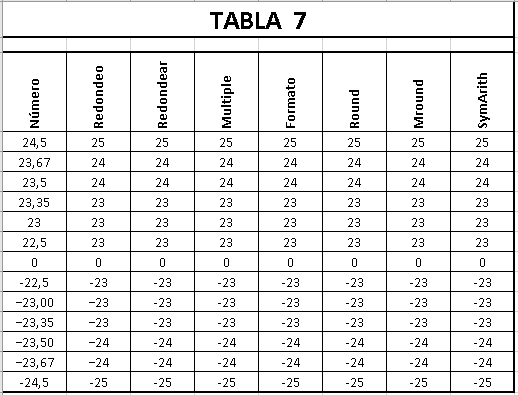
Este método trata los valores
positivos y negativos
simétricamente y por lo tanto no
habrá sesgo (por mejor decir, la
tendencia es a que no haya
sesgo) si los números positivos
y negativos están equilibrados,
pero en el caso de que
predominen unos u otros, el
sesgo existirá (si predominan
los positivos el sesgo será por
exceso y si predominan los
negativos el sesgo será por
defecto).
Esta regla se utiliza
habitualmente para conversiones
de números y redondeo de precios
(esto garantiza el mismo trato
para los pagos y para los
cobros).
Desempate la mitad hacia el cero
(Round Half Towards Zero o
Round Half Away From Infinity)
No existe ninguna función Excel que realice este redondeo.
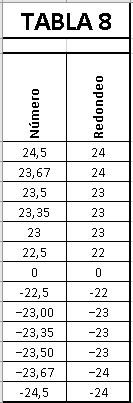
Este método es similar al
anterior y lo dicho es de
aplicación mutatis mutandi.
Desempate la mitad al par (Round
Half To Even) que es el
entero par más cercano a y.
No existe ninguna función Excel
ni VBA que haga este redondeo.
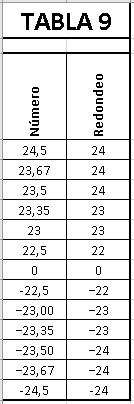
Este método trata los valores
positivos y negativos
simétricamente, y está por eso,
libre del sesgo del signo. Mejor
aún, para razonables
distribuciones de valores de y,
el valor esperado de los números
redondeados es el mismo que el
de los números originales. Sin
embargo, esta regla introduce un
sesgo hacia el cero en los
números pares y un sesgo hacia
infinito en los números impares.
Esta variante de redondeo al más
cercano, también se llama
redondeo sin sesgo (Unbiased
Rounding), redondeo
convergente (Convergent
Rounding), redondeo
estadístico (Statistician's
Rounding), redondeo holandés
(Dutch Rounding),
redondeo gausiano (Gaussian
Rounding), redondeo
par-impar (Odd-Even Rounding)
o redondeo del banquero (Bankers'
Rounding), y es ampliamente
usado en contabilidad.
Este es el método usado en las
funciones y operadores de la
aritmética de punto flotante
usada en IEEE 754.
Desempate la mitad hacia el
impar (Round Half To Odd)
que es el entero impar más
cercano a y.
No existe ninguna función Excel ni VBA que haga este redondeo.
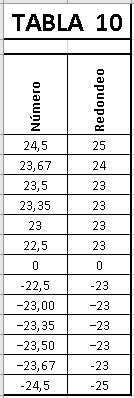
Este método también trata los
valores positivos y negativos
simétricamente, y está por eso,
libre del sesgo del signo. Mejor
aún, para distribuciones
razonables de valores de y, el
valor (medio) esperado de los
números redondeados es el mismo
que el de los números
originales. Sin embargo, esta
regla introducirá un sesgo hacia
infinito para los números pares
y un sesgo hacia cero, para los
números impares.
Esta variante no es usada casi
nunca en computación, excepto en
situaciones donde se quiere
evitar redondear
0,5
o
−0,5
a cero; o para evitar
incrementar la escala (el
exponente) en los números de
punto flotante, que tienen un
rango de exponentes limitado.
Desempate estocástico (Stochastic
Rounding)
Otro método de desempate no
sesgado es el redondeo
estocástico (Stochastic
Rounding):
Si la parte fraccionaria de y es
.5, escoge que aleatoriamente
entre y + 0.5 e y − 0.5, con
igual probabilidad.
Como el redondeo la mitad hacia
el par (Round-Half-To-Even),
este método no sólo está libre
de sesgo, sino que también
reparte equitativamente que
entre valores pares e impares.
En contra, introduce un
componente aleatorio en el
resultado; si hacemos el mismo
cálculo dos veces, podemos
obtener dos resultados
diferentes. También, es propenso
a que los humanos (más que de
los computadores o dispositivos
elegidos) subconscientemente
están “aleatoriamente”
decidiendo en que dirección
redondear.
Ningún producto de Microsoft
implementa este método de
desempate. La función
personalizada RandRound,
realiza este redondeo.
Desempate alternando (Alternating
Tie-Breaking)
Un método, más oscuro que la
mayoría, es redondear la mitad
(el 5) alternativamente (Round
Half Alternatingly).
Si la parte fraccionaria es 0,5,
alternar el redondeo hacia
arriba y hacia abajo: para el
primer caso de una fracción
terminada en 5, redondear hacia
arriba; para la segunda
ocurrencia, hacia abajo; y así,
sucesivamente.
Esto suprime el componente
aleatorio del resultado, si los
casos con parte fraccionaria en
0,5 se pueden numerar. Pero
puede todavía introducir un
sesgo positivo o negativo (en
función del redondeo inicial) al
redondeo
si el número total de
casos es impar.
Ningún producto de Microsoft
implementa este método de
desempate. La función
personalizada AltRound,
realiza este redondeo.
DOBLE REDONDEO
Redondear un número dos veces en sucesión a diferentes precisiones, con la última menos precisa, no garantiza que se obtenga el mismo resultado que redondear una vez con la precisión final, excepto en el caso de redondeo directo. Por ejemplo, redondear 9,46 a un decimal da 9.5, y luego 10 cuando redondeamos a entero usando redondeo mitad al par, pero daría 9 cuando redondeamos a entero directamente.
RESUMEN MÉTODOS DE REDONDEO
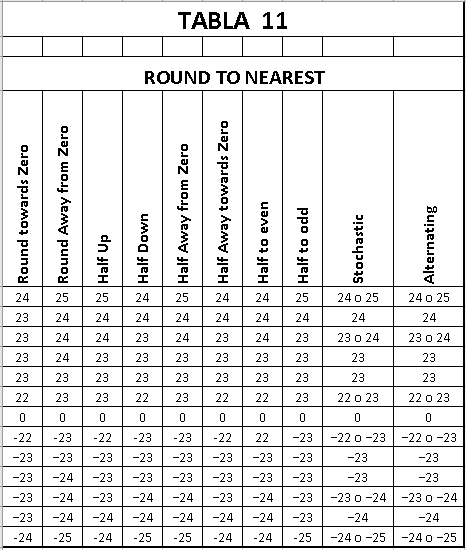
FUNCIONES DE REDONDEO DE VBA
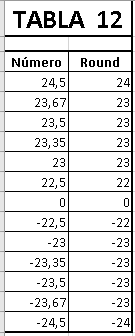
La única función, en sentido
estricto, de VBA es Round(). Las
funciones Int(), Fix(), CInt(),
CLng(), sólo convierten a
números enteros, por lo que no
son, propiamente, funciones de
redondeo.
La función Round de VBA no es
igual que la función REDONDEAR
de Excel y Round de VBA Excel.
MÉTODOS DE REDONDEO DE EXCEL
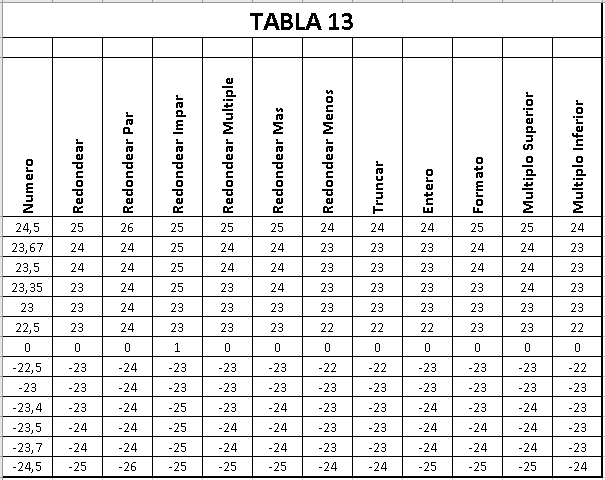
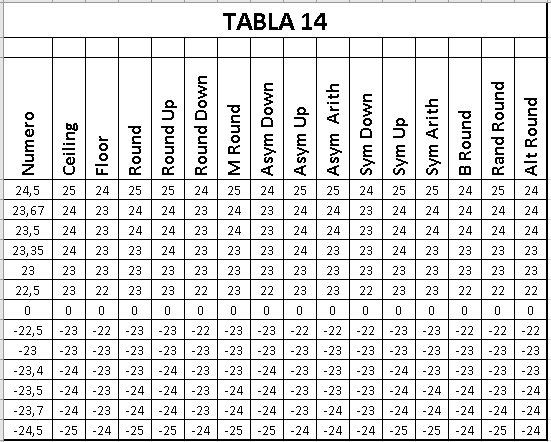
CÓDIGOS UTILIZADOS
Function AsymDown(ByVal
X As Double, Optional ByVal
Factor As Double = 1) As Double
' Asymmetrically rounds numbers
down - similar to Int().
' Negative numbers get more
negative.
AsymDown = Int(X *
Factor) / Factor
End Function
Function SymDown(ByVal
X As Double, Optional ByVal
Factor As Double = 1) As Double
' Symmetrically rounds numbers
down - similar to Fix().
' Truncates all numbers toward
0.
' Same as AsymDown for positive
numbers.
SymDown = Fix(X * Factor)
/ Factor
' Alternately:
' SymDown = AsymDown(Abs(X),
Factor) * Sgn(X)
End Function
Function AsymUp(ByVal
X As Double, Optional ByVal
Factor As Double = 1) As Double
' Asymmetrically rounds numbers
fractions up.
' Same as SymDown for negative
numbers.
' Similar to Ceiling.
Dim Temp As Double
Temp = Int(X * Factor)
AsymUp = (Temp + IIf(X =
Temp, 0, 1)) / Factor
End Function
Function SymUp(ByVal
X As Double, Optional ByVal
Factor As Double = 1) As Double
' Symmetrically rounds fractions
up - that is, away from 0.
' Same as AsymUp for positive
numbers.
' Same as AsymDown for negative
numbers.
Dim Temp As Double
Temp = Fix(X * Factor)
SymUp = (Temp + IIf(X =
Temp, 0, Sgn(X))) / Factor
End Function
Function AsymArith(ByVal
X As Double, Optional ByVal
Factor As Double = 1) As Double
' Asymmetric arithmetic rounding
- rounds .5 up always.
' Similar to Java worksheet
Round function.
AsymArith = Int(X *
Factor + 0.5) / Factor
End Function
Function SymArith(ByVal
X As Double, Optional ByVal
Factor As Double = 1) As Double
' Symmetric arithmetic rounding
- rounds .5 away from 0.
' Same as AsymArith for positive
numbers.
' Similar to Excel Worksheet
Round function.
SymArith = Fix(X * Factor
+ 0.5 * Sgn(X)) / Factor
' Alternately:
' SymArith = Abs(AsymArith(X,
Factor)) * Sgn(X)
End Function
Function BRound(ByVal
X As Double, Optional ByVal
Factor As Double = 1) As Double
' Banker's rounding.
' Rounds .5 up or down to
achieve an even number.
' Symmetrical by definition.
' For smaller numbers:
' BRound = CLng(X * Factor) /
Factor
Dim Temp As Double
Dim FixTemp As Double
Temp = X * Factor
FixTemp = Fix(Temp + 0.5
* Sgn(X))
' Handle rounding of .5
in a special manner
If Temp - Int(Temp) = 0.5
Then
If FixTemp / 2 <> Int(FixTemp
/ 2) Then
' Is Temp odd
' Reduce Magnitude by 1
to make even
FixTemp = FixTemp - Sgn(X)
End If
End If
BRound = FixTemp / Factor
End Function
Function RandRound(ByVal
X As Double, Optional ByVal
Factor As Double = 1) As Double
' Random rounding.
' Rounds .5 up or down in a
random fashion.
' Should Execute Randomize
statement somewhere prior to
calling.
Dim Temp As Double,
FixTemp As Double
Temp = X * Factor
FixTemp = Fix(Temp + 0.5
* Sgn(X))
' Handle rounding of .5
in a special manner.
If Temp - Int(Temp) = 0.5
Then
' Reduce Magnitude by 1
in half the cases.
FixTemp = FixTemp - Int(Rnd
* 2) * Sgn(X)
End If
RandRound = FixTemp /
Factor
End Function
Function AltRound(ByVal
X As Double, Optional ByVal
Factor As Double = 1) As Double
' Alternating rounding.
' Alternates between rounding .5
up or down.
Static fReduce As Boolean
Dim Temp As Double,
FixTemp As Double
Temp = X * Factor
FixTemp = Fix(Temp + 0.5
* Sgn(X))
' Handle rounding of .5
in a special manner.
If Temp - Int(Temp) = 0.5
Then
' Alternate between
rounding .5 down (negative) and
up (positive).
If (fReduce And Sgn(X) =
1) Or (Not fReduce And Sgn(X) =
-1) Then
' Or, replace the
previous If statement with the
following to
' alternate between
rounding .5 to reduce magnitude
and increase
' magnitude.
' If fReduce Then
FixTemp = FixTemp - Sgn(X)
End If
fReduce = Not fReduce
End If
AltRound = FixTemp /
Factor
End Function
Function ADownDigits(ByVal
X As Double, Optional ByVal
Digits As Integer = 0) As Double
' sample wrapper functions
ADownDigits = AsymDown(X,
10 ^ Digits)
End Function
'Function Ceiling2(ByVal X As
Double, Optional ByVal Factor As
Double = 1) As Double
'
Ceiling2 =
Application.WorksheetFunction.Ceiling(X,
Factor)
'End Function
'
'Function Floor2(ByVal X As
Double, Optional ByVal Factor As
Double = 1) As Double
'
Floor2 =
Application.WorksheetFunction.Floor(X,
Factor)
'End Function
'
'Function Round2(ByVal X As
Double, Optional ByVal Factor As
Double = 1) As Double
'
Round2 =
Application.WorksheetFunction.Round(X,
Factor)
'End Function'
'
'Function RoundUp2(ByVal X As
Double, Optional ByVal Factor As
Double = 1) As Double
'
RoundUp2 =
Application.WorksheetFunction.RoundUp(X,
Factor)
'End Function
'
'Function RoundDown2(ByVal X As
Double, Optional ByVal Factor As
Double = 1) As Double
'
RoundDown2 =
Application.WorksheetFunction.RoundDown(X,
Factor)
'End Function
'
'Function MRound2(ByVal X As
Double, Optional ByVal Factor As
Double = 1) As Double
'
MRound2 =
Application.WorksheetFunction.MRound(X,
Factor)
'End Function
Consulta también:
![]() https://en.wikipedia.org/wiki/Rounding
https://en.wikipedia.org/wiki/Rounding